My current research involves the modeling of certain types of human activity that exhibit regular spatio- and/or temporal patterns.  As a case study, we have generally focused on various types of criminal behavior, since there are clear patterns in this activity and we have access to relatively large amounts of data.  A large portion of this work aims to model the formation and dynamics of crime "hotspots" - spatio-temporal regions of increased criminal activity. Working with data provided by the Los Angeles and Long Beach police departments, we have developed methods of measuring the repeat and near-repeat criminal events that are the hallmarks of hotspot formation. 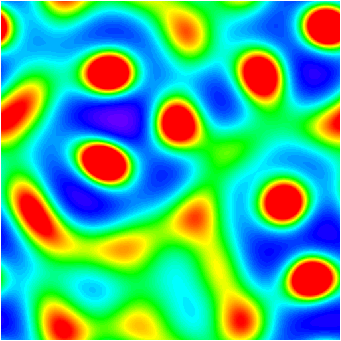We have also constructed a family of discrete models that allow for such patterns to develop from natural criminal behavior, and have derived continuum approximations of these discrete models. Some output from one of many simulations (right) illustrates this finding, with "hot" areas in red and "cold" areas in purple.

In addition to the work on crime hotspots, this overarching project has also included: more accurate predictions of when and where crimes will occur, based on self-exciting point process models borrowed from seismology; the study of gang territoriality, modeled via diffusive Lotka-Volterra equations;  gang retaliatory violence, and how the police may be able to solve such crimes using constrained optimization; the evolution of gang rivalry networks in the presence of retaliation and third-party effects; game theoretic models for the levels of both crime and cooperation with the authorities in society; and new methods for finding the "anchor points" of criminals given the locations of crimes they committed, based on models inspired by animal foraging.  Please see my publications page for prints of all these works and more.

This work is being done in collaboration with Jeff Brantingham, Andrea Bertozzi, Lincoln Chayes, George Tita, George Mohler, Maria D'Orsogna, and others.

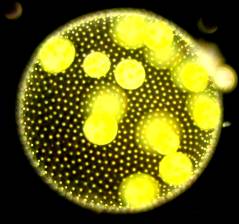For many species of aquatic microorganisms (such as Volvox, pictured to the left), diffusion alone cannot supply nutrition at a rate high enough to keep the organism alive if the size of the organism exceeds a critical value.  These organisms can get around this evolutionary bottleneck by using flagella to swim in their aqueous surroundings, thereby bringing advection into the picture.  This advection effectively "stirs" the solution, greatly increasing the nutrient uptake rate, which allows the organisms to continue to evolve to ever greater sizes.  In addition, for the specific example of Volvox, this adaptation necessitates the transition from species with only one type of cell to those in which cell specialization exists.  Our work in this area models these various processes for the many species of Volvox.  We use experimental measurements to validate our models and find that our predicted bottleneck radius, at which cell specialization must occur, is very close to the actual size in which this adaptation is observed.

This work was a part of my PhD thesis and was done in collaboration with Cristian Solari, Sujoy Ganguly, Thomas Powers, John Kessler, and Raymond Goldstein.

Though the general processes underlying the formation of stalactites and icicles have long been known, it was unclear how these processes eventually led to the iconic carrot-like shape often associated with these objects.  This research project modeled the growth of both stalactites and icicles as free-boundary problems, arriving at growth laws for each of these objects.  Interestingly, these growth laws are scale invariant, implicating that there is in fact a single platonic ideal shape for both stalactites (picture at right) and icicles.  Even more interestingly, the mathematical form for the ideal stalactite is the same as that for the ideal icicle far from the tip, even though the growth processes underlying these two structures are vastly different.

This work was a part of my PhD thesis and was done in collaboration with Jim Baygents, Warren Beck, David Stone, Rick Toomey, and Raymond Goldstein.